Statistics

Mixed

Author

Sungkyun Cho

Published

February 11, 2023

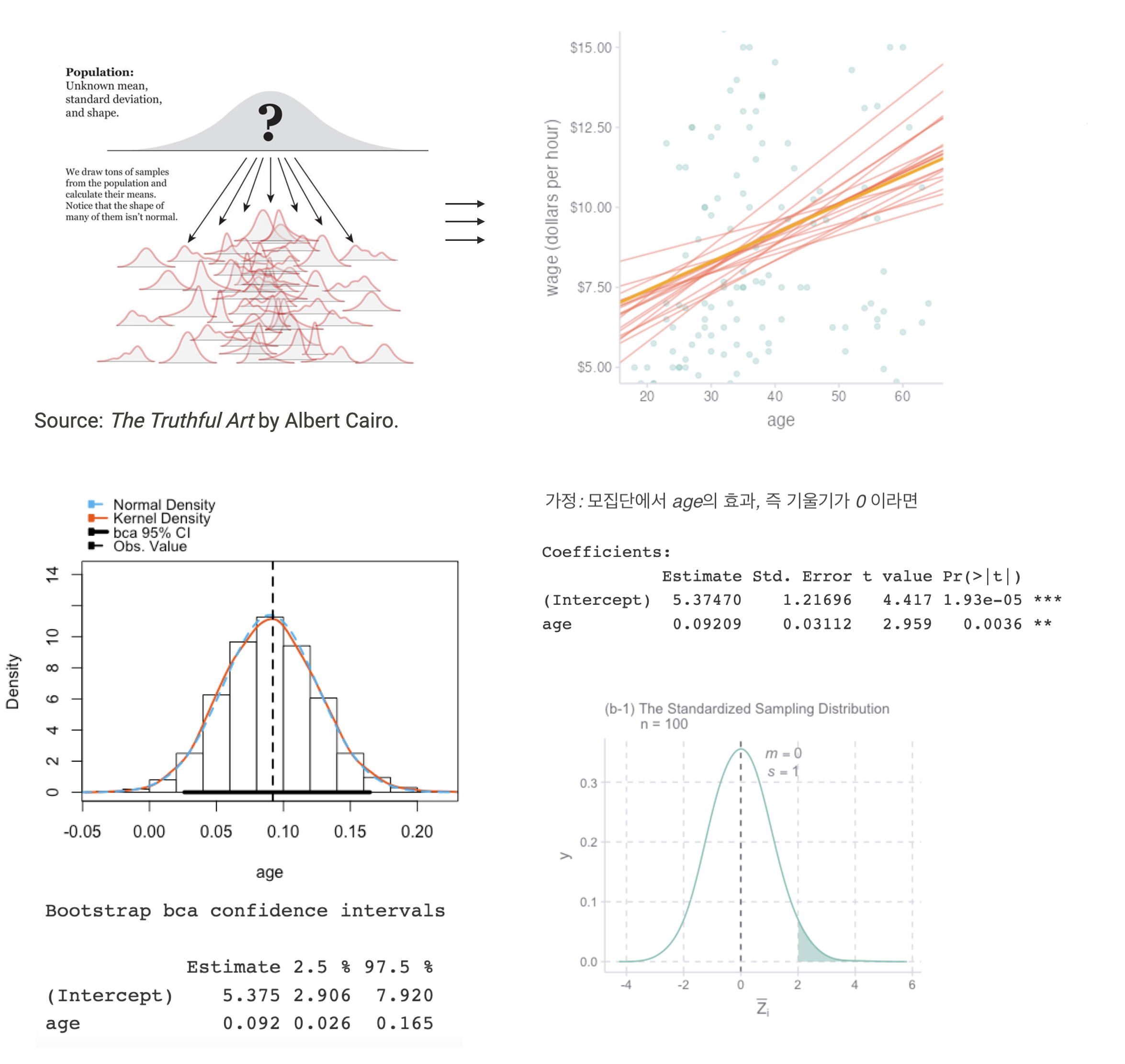
선형 관계에 기반한 모형

예측 모형 vs. 인과 모형

Regression analysis

Case 1

Source: Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences (3rd ed.)

교수의 연봉(salary)이 학위를 받은 후 지난 시간(time since Ph.D.)과 출판물의 수(pubs)에 의해 어떻게 영향을 받는가?

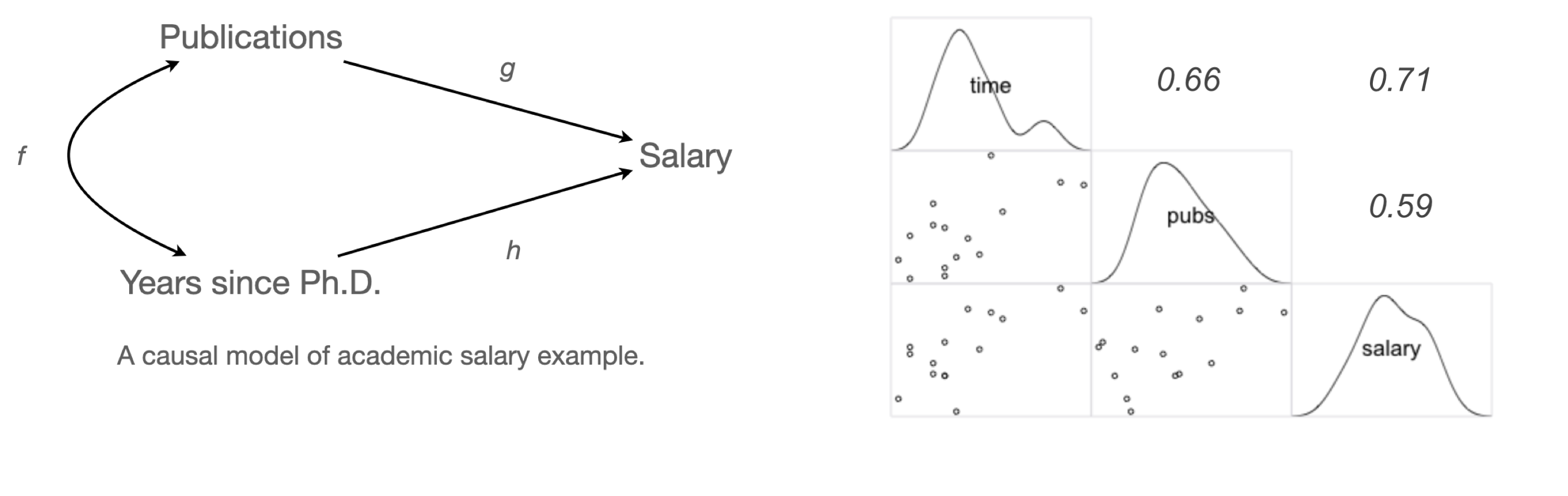
Data: c0301dt.csv

acad0 = pd.read_csv("data/c0301dt.csv")
acad0.head(5)
   time  pubs  salary
0     3    18   51876
1     6     3   54511
2     3     2   53425
3     8    17   61863
4     9    11   52926
from statsmodels.formula.api import ols

mod1 = ols("salary ~ time", data = acad0).fit()
mod2 = ols("salary ~ pubs", data = acad0).fit()
mod3 = ols("salary ~ time + pubs", data = acad0).fit()

세 모형을 비교하면,

Model 1: \(\widehat{salary} = \$1,224\:time + \$43,659\)
Model 2 : \(\widehat{salary} = \$336\:pubs + \$46,357\)
Model 3: \(\widehat{salary} = \$983\:time + \$122\:pubs + \$43,082\)

  • 연차(time)의 효과는 $1,224에서 $984로 낮아졌고,
  • 논문수(pubs)의 효과는 $336에서 $122로 낮아졌음.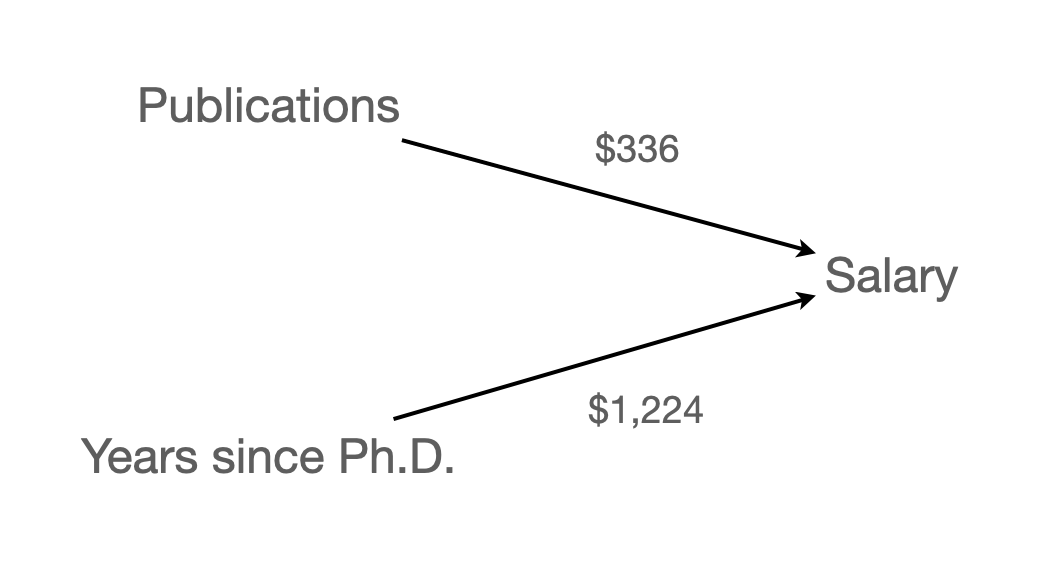

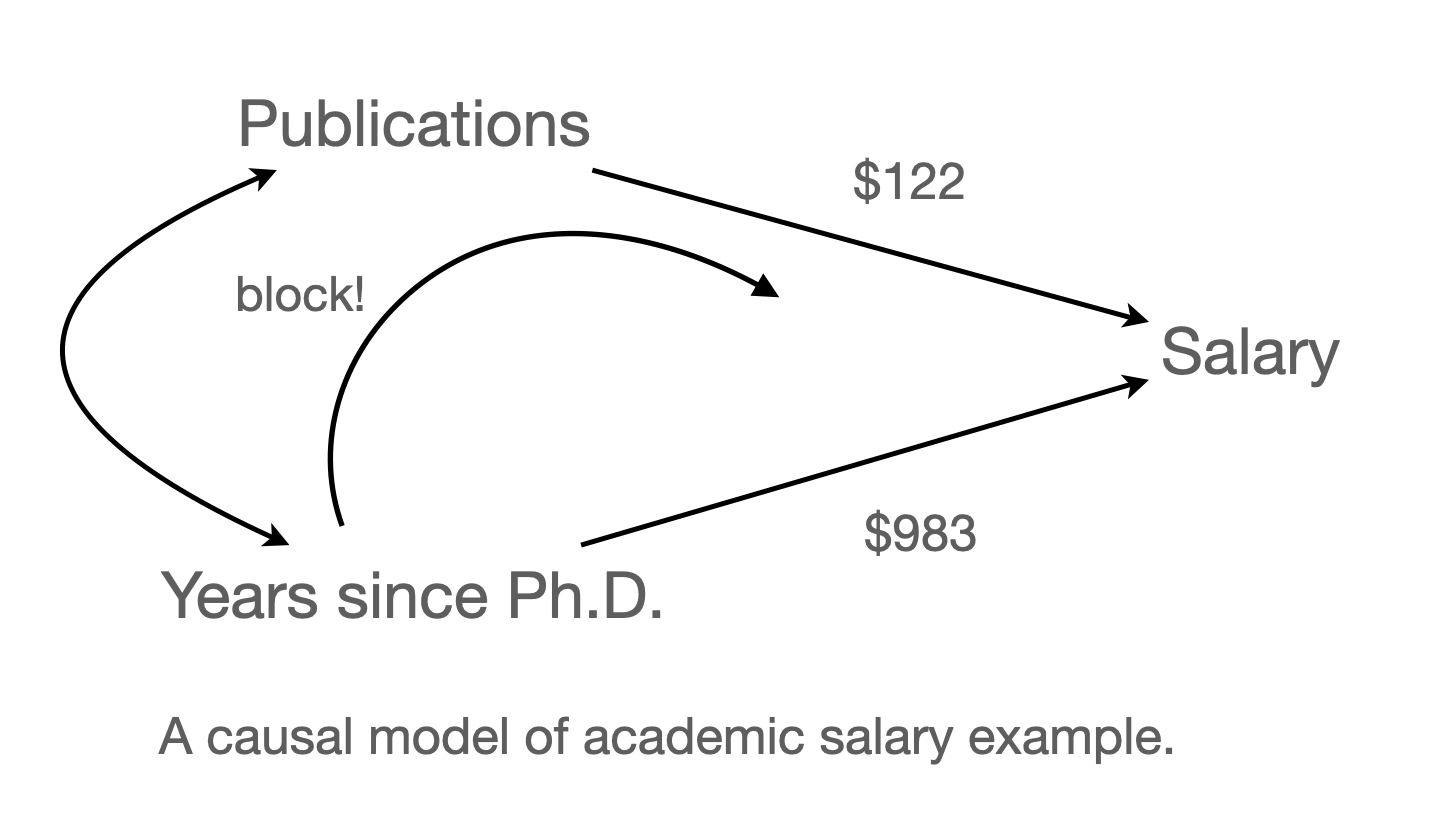
  • 교수들의 연차와 그들이 쓴 논문 수는 깊이 연관되어 있으며 (r = 0.66), 두 변수의 redunancy가 각 변수들의 효과를 변화시킴.
  • 두 예측 변수의 산술적 합으로 연봉을 예측하므로 각 예측변수의 효과는 수정될 수 밖에 없음.
  • 수학적으로 보면, 각 예측변수의 기울기는 다른 예측변수의 값에 상관없이 일정하므로, 다른 예측변수들을 (임의의 값에) 고정시키는 효과를 가짐
  • 즉, 다른 변수와는 독립적인, 고유한 효과를 추정하게 됨

각 회귀계수를 partial regression coefficient (부분 회귀 계수) 라고 부름.

부분 회귀 계수의 첫번째 해석:

  • 만약 논문 수가 일정할 때, 예를 들어 10편의 논문을 쓴 경우만 봤을 때, 연차가 1년 늘 때마다 연봉은 $984 증가함; 평면의 선형모형을 가정했기에 이 관계는 논문 수에 상관없음.
  • 연차가 일정할 때, 예를 들어 연차가 12년차인 경우만 봤을 때, 논문이 1편 늘 때마다 연봉은 $336 증가함; 평면의 선형모형을 가정했기에 이 관계는 연차에 상관없음.

이는 다른 변수를 고려 (통제, controlling for) 했을 때 혹은 다른 변수의 효과를 제거 (partial out) 했을 때, 각 변수의 고유한 효과를 의미함; holding constant, controlling for, partialing out, adjusted for, residualizing

뒤집어 말하면, 연차만 고려했을때 연차가 1년 늘면 $1,224 연봉이 증가하는 효과는 연차가 늘 때 함께 늘어나는 논문 수의 효과가 함께 섞여 나온 효과라고 말할 수 있음.

이는 인과관계에 있는 변수들의 진정한 효과를 찾는 것이 얼마나 어려운지를 보여줌

부분 회귀 계수에 대한 두번째 해석

  • 다른 변수들이 partial out 된 후의 효과.
  • 실제로 $122는 연차로 (선형적으로) 예측/설명되지 않는 논문수(residuals)로 [연차로 예측/설명되지 않는] 연봉을 예측할 때의 기울기

 

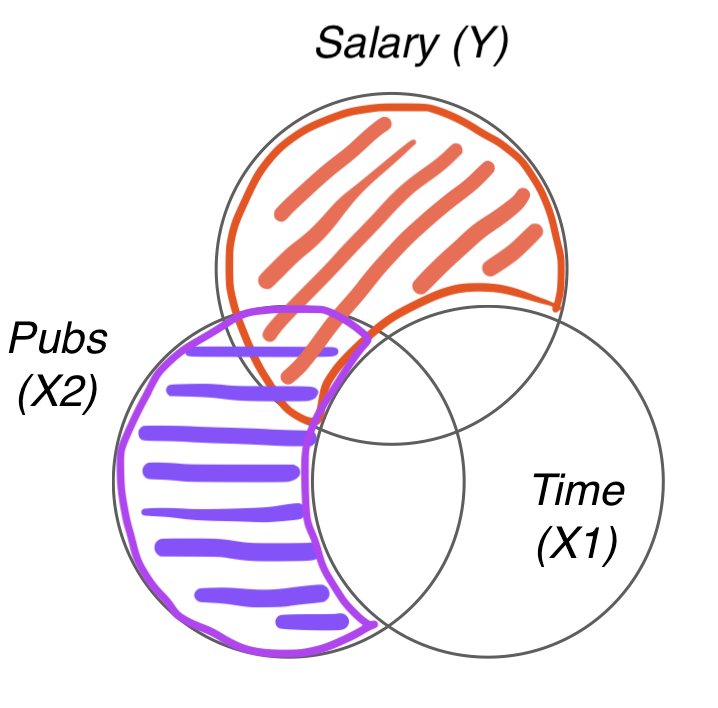
Diamonds의 예

Direct and Indirect Effects

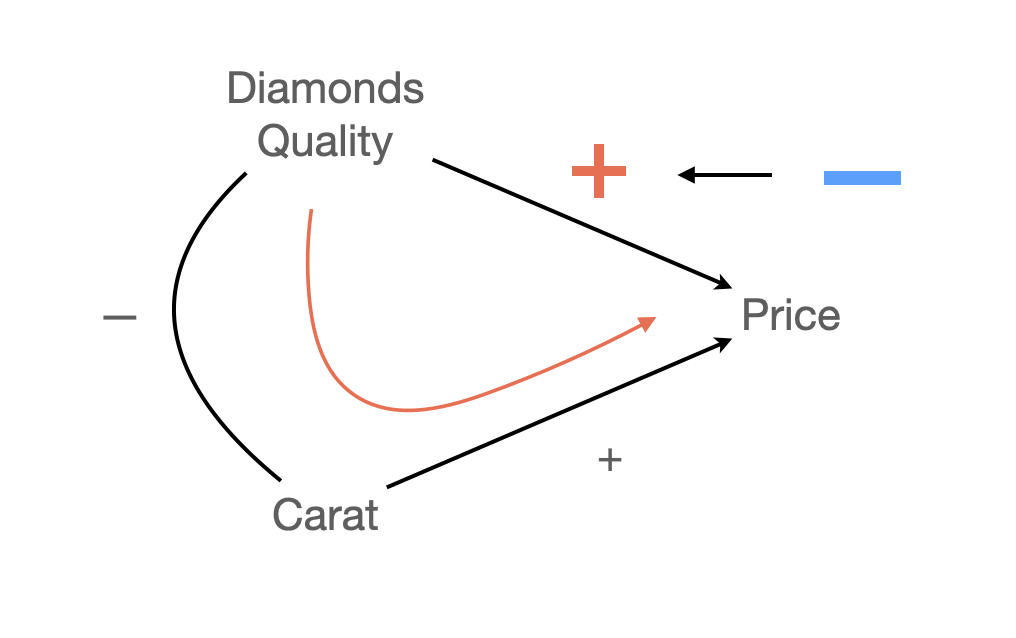
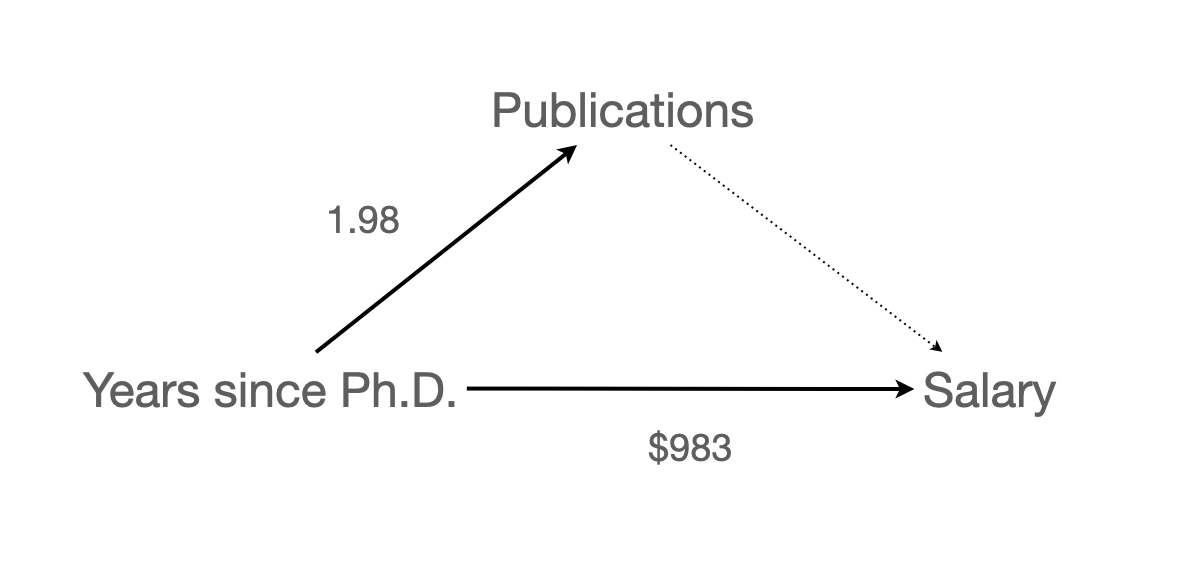
만약, 다음과 같은 인과모형을 세운다면,

  • 연차가 연봉에 미치는 효과가 두 경로로 나뉘어지고,
  • 연차 \(\rightarrow\) 연봉: 직접효과 $983
  • 연차 \(\rightarrow\) 논문 \(\rightarrow\) 연봉: 간접효과 1.98 x $122 = $241.56
  • 두 효과를 더하면: $983 + $241.56 = $1224.56 = 논문수를 고려하지 않았을 때 연차의 효과
    • 즉, 연차가 1년 늘때 연봉이 $1224 증가하는 것은 연차 자체의 효과($983)와 논문의 증가에 따른 효과($241)가 합쳐져 나온 결과라고 말할 수 있음.
  • 이 때, 논문의 수가 연차와 연봉의 관계를 매개(mediate)한다고 표현.

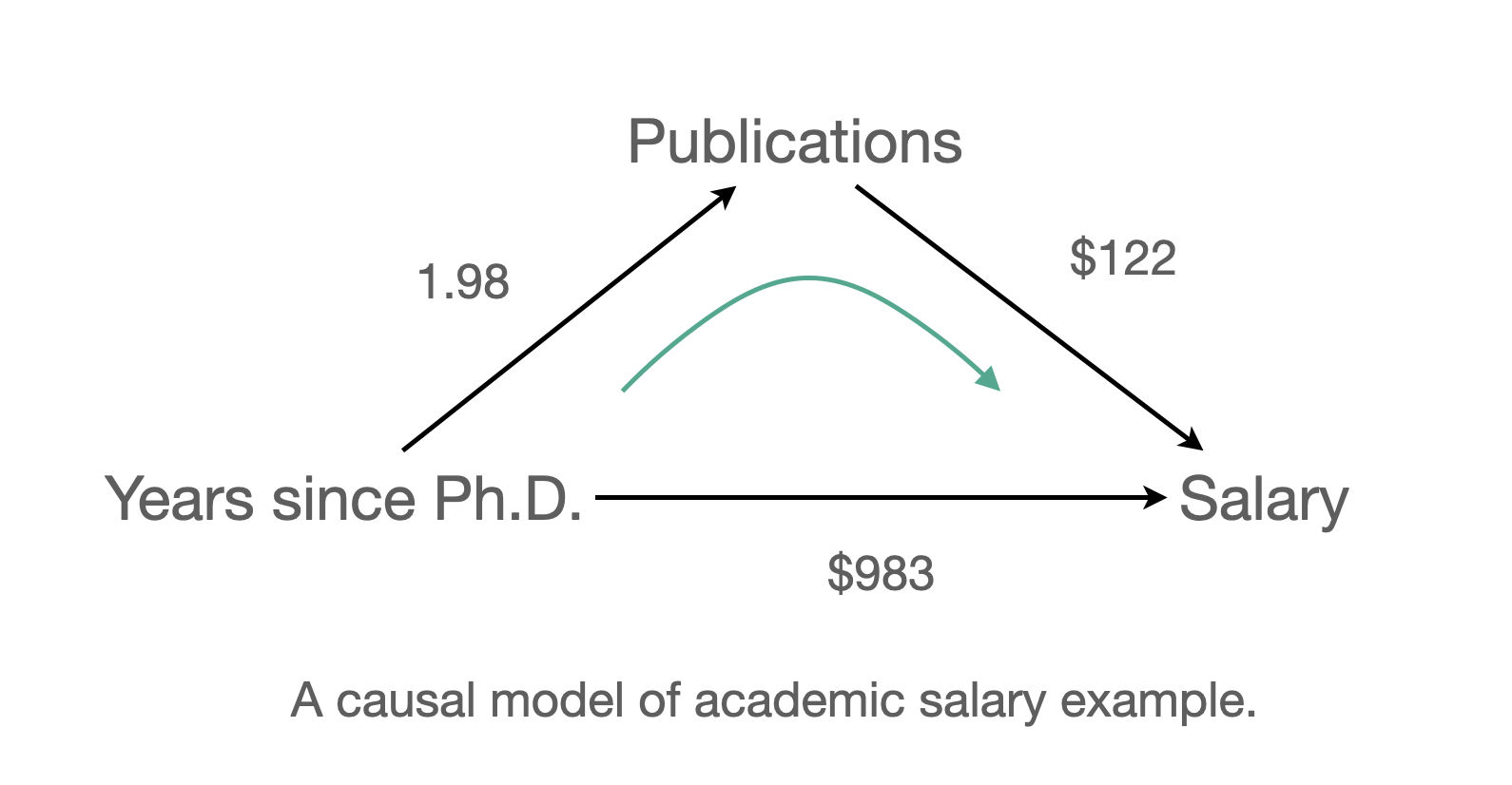
만약, 연차의 효과 $1224이 논문수를 고려했을 때 줄어든($983) 수준을 훨씬 넘어 통계적으로 유의하지 않을 정도로 0에 가까워진다면, 연차의 효과는 모두 논문의 효과를 거쳐 나타나는 것이라고 말할 수 있음. 이 때, 완전 매개 (fully mediate)한다고 표현함.

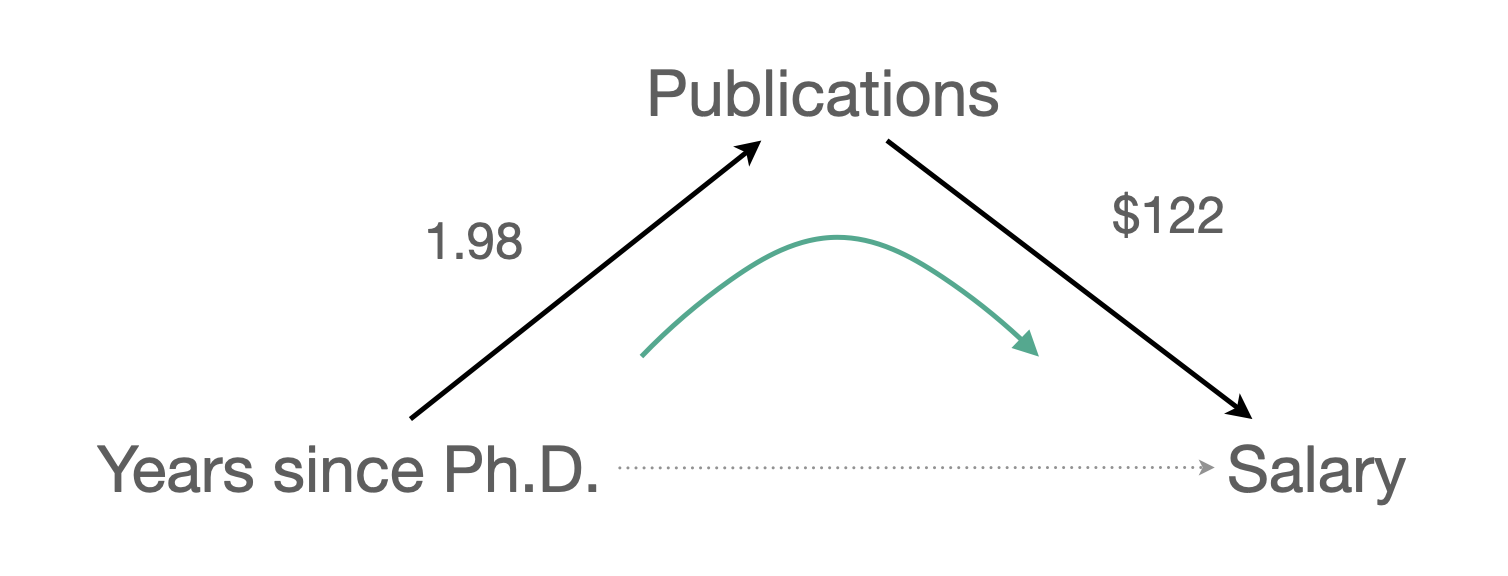
이들는 인과관계의 기제/메커니즘의 일부를 설명해 줌.

반대로, 만약 다음과 같이 논문의 효과가 거의 사라진다면, 논문의 효과는 가짜 효과, spurious effect라고 표현함. 이는 논문과 연봉 간의 관계가 보이는 이유는 연차라는 common cause가 연결하고 있기 때문임. 이를 confounding이라고 함.

신발을 신고 잠든 다음날 두통이 생긴다면?


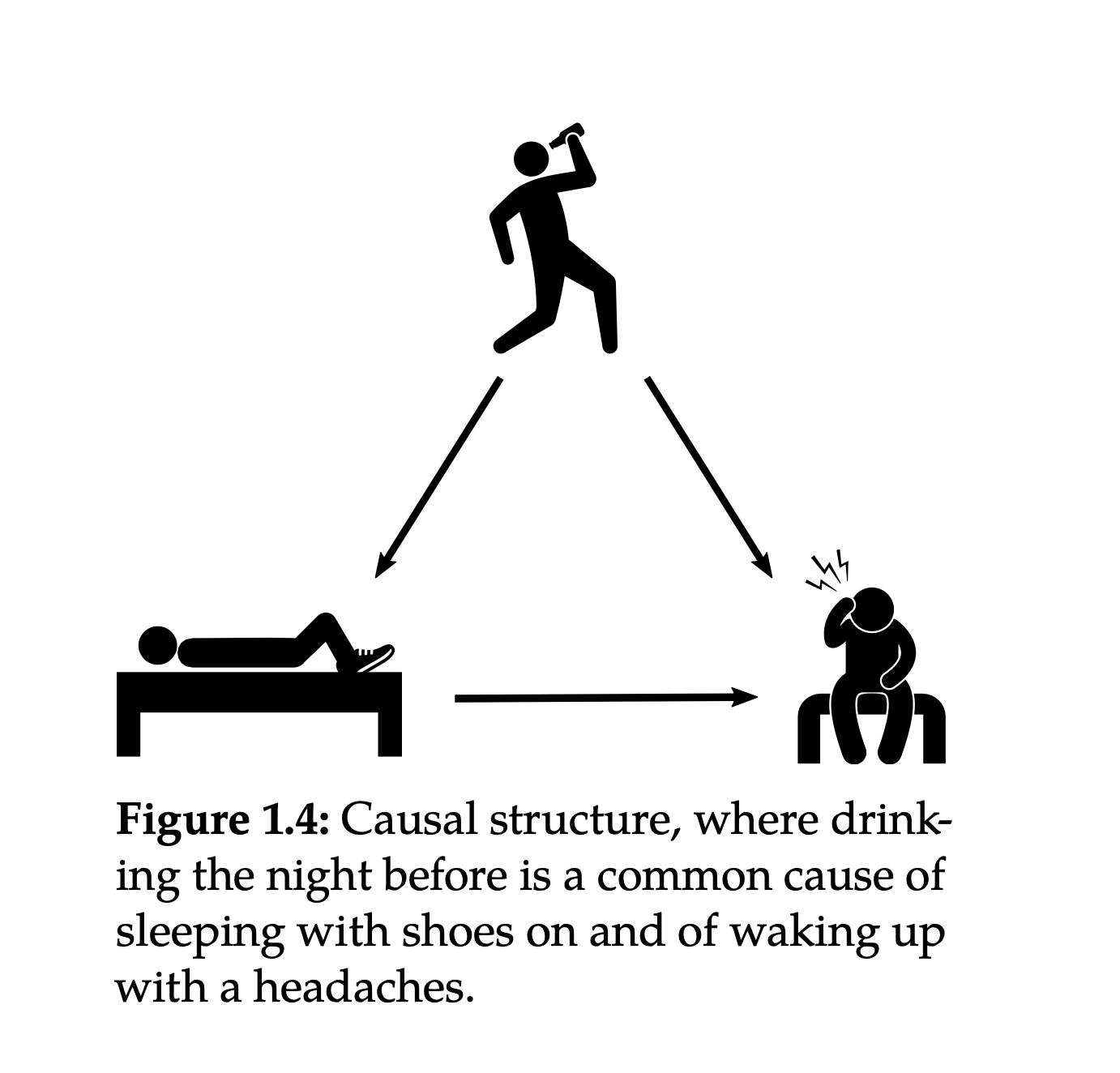
Source: Introduction to Causal Inference (ICI) by Brady Neal

Confounding

일반적으로, 표면적으로 드러난 변수간의 관계가 숨겨진 다른 변수(lurking third variable)에 의해 매개되어 있어 진실한 관계가 아닌 경우, confounding 혹은 confounder가 존재한다고 함.
사회과학에서 오래된 가장 핵심적인 문제이나 최근까지도 정확히 정의하기 어려움 개념이었음.
Causal analysis라는 통계와는 별개의 개념으로 발전되어 최근에야 이론적으로 완성이 되어 관심이 높아짐.

극단적이지만 이해하지 쉬운 예로는

  • 초등학생 발 사이즈 → 독해력
  • 머리 길이 → 우울증

Simpson’s paradox

아래 첫번째 그림은 집단 전체에 대한 플랏이고, 두번째 그림은 나이대별로 나누어 본 플랏
전체 집단을 보면 운동을 많이 할수록 콜레스테롤이 증가하는 것으로 보이나,
나이대별로 보면, 상식적으로 운동이 긍정적 효과가 나타남.
왜 그렇게 나타나는가?


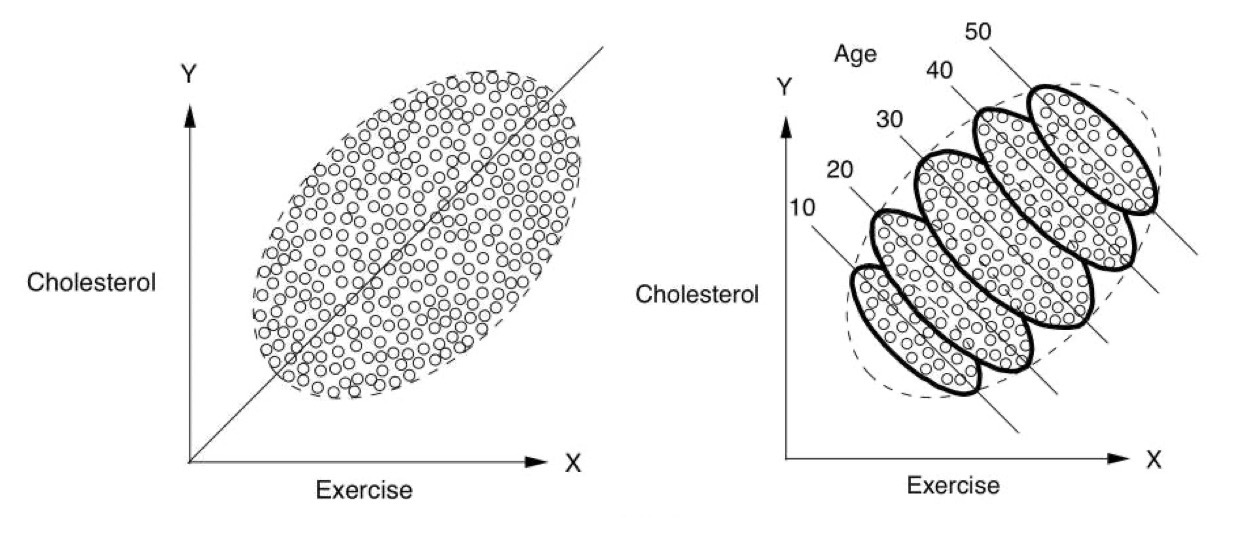
Source: The book of why by Judea Pearl

관찰 데이터로부터 진정한 관계를 파악하기 위해서는 이와 같은 통계적인 통제를 통해 혹은 인과분석이라는 좀 더 큰 프레임에서 분석해야 하며, 깊은 논의가 필요함

예를 들면,
은퇴한 노인들을 대상으로 규칙적인 걷기가 사망율을 감소시킬 것이라는 가설을 확인하기 위해 1965년 이후 8000명 가량의 남성들을 추적조사한 데이터의 일부를 이용했는데,
Source: The book of why by Judea Pearl

  • 12년 후 사망율에서 casual walker(하루 1마일 이하)와 intense walker(하루 2마일 이상)가 각각 43%, 21.5%로 나타났음.
  • 이 걷기의 효과를 의심케 하는 요소들(confounding)은 무엇인가?
  • 건강이 나빠 많이 걷지 못했을 수도…
  • 많이 걷는 사람은 상대적으로 젊을 수도…
  • 많이 먹는 사람이 덜 걸을 수도…
  • 술을 많이 먹는 사람이 덜 걸을 수도…

Case 2

Source: Introduction to Causal Inference (ICI) by Brady Neal

COVID-27

Case 3

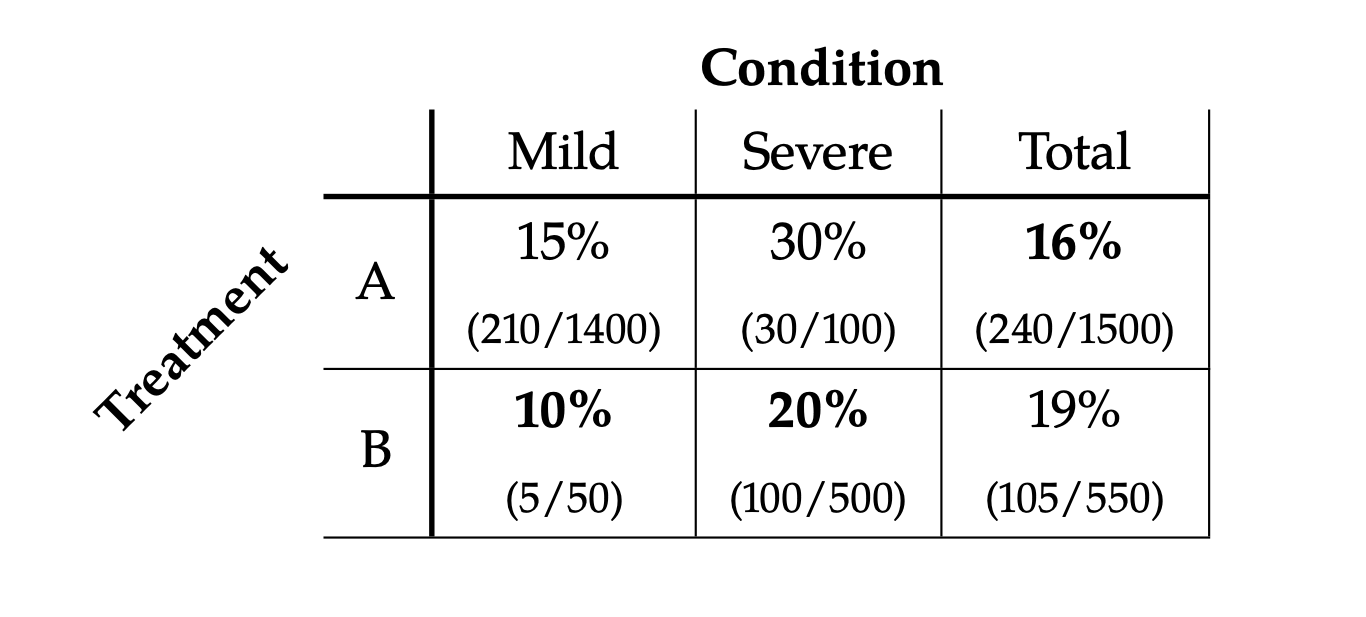
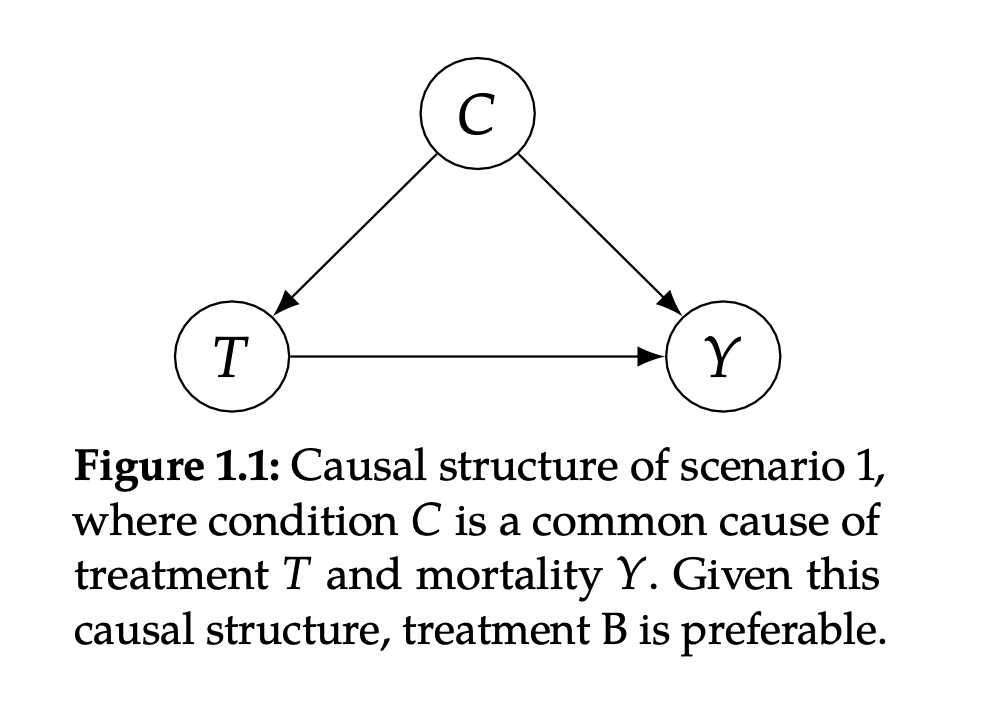
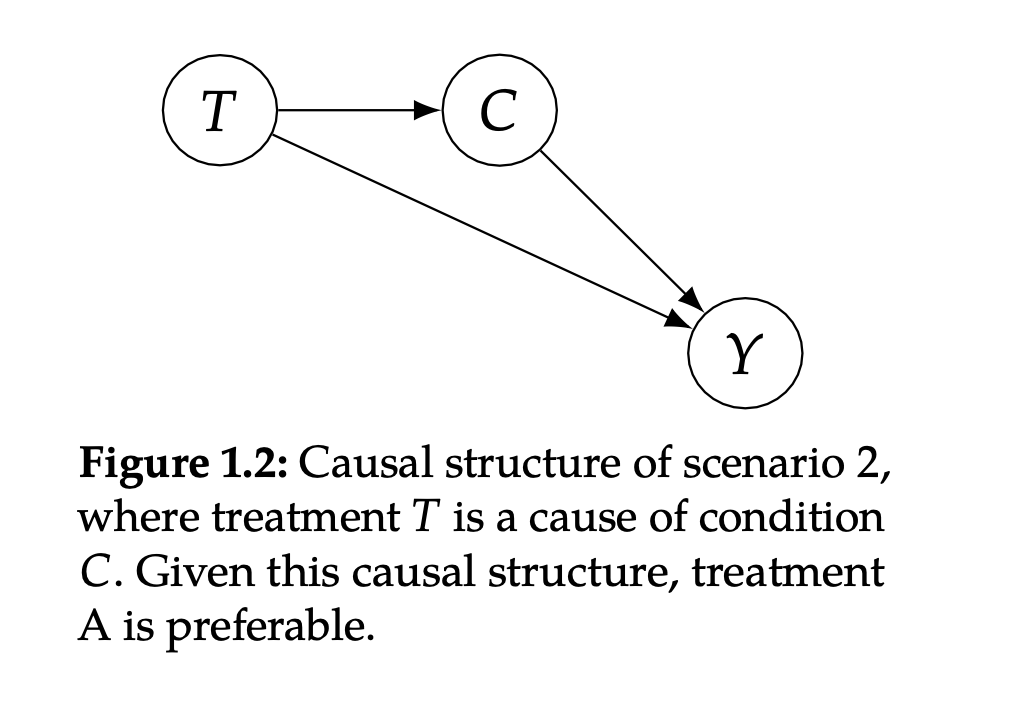
Source: Multiple Regression and Beyond (3e) by Timothy Z. Keith

National Education Longitudinal Study of 1988 (NELS:88)

학생들의 과제는 성적에 영향을 주는가? 준다면 그 영향력의 크기는 어떠한가?

Colider

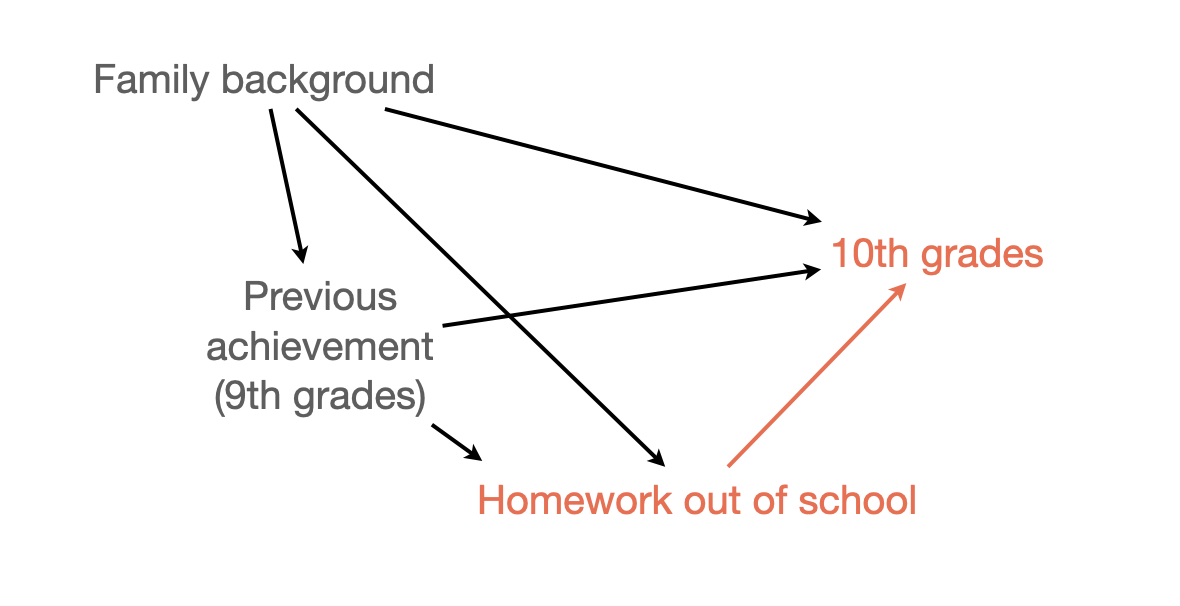
운동능력이 뛰어나면 지능이 떨어지는가?

Cognitive Bias

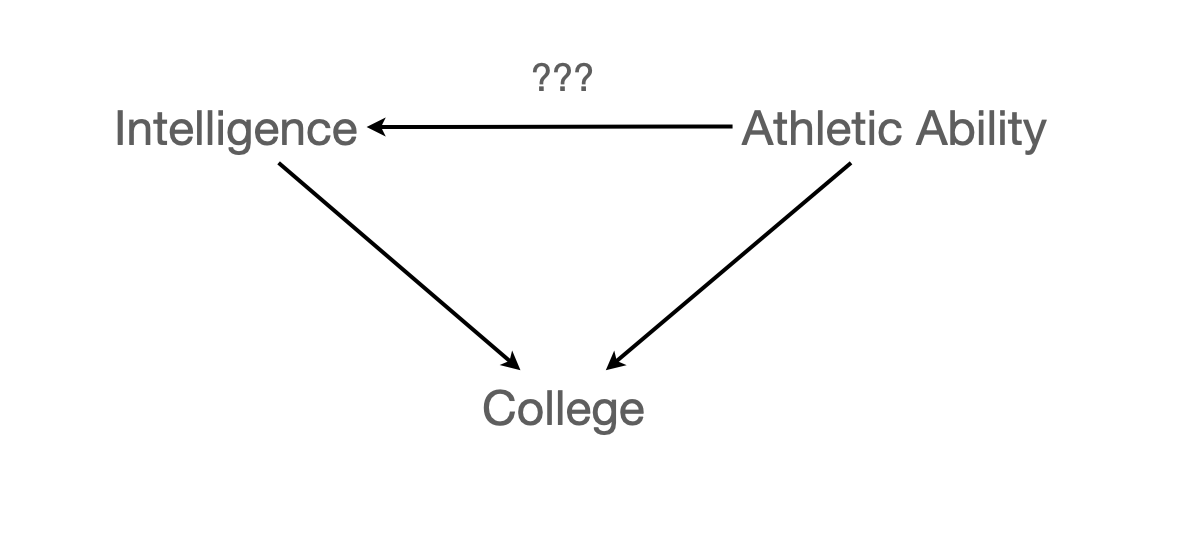
관계성(correlation)으로부터 인과관계(causation)를 끌어내려는 매우 높은 경향성이 존재

  • Availability huristic: 쉽게 떠올릴 수 있는 사례들로부터 추론; ex. 커피를 마셔서?
  • Motivated reasoning: 자신의 믿음을 뒷받침하기 위해 증거를 찾는 것; ex. 데이터분석을 너무 많이 해서?

  

Causal Inference

기존 통계학의 개념을 넘어서 인과관계를 파악하기 위한 새로운 프레임워크

The Fundamental Problem of Causal Inference


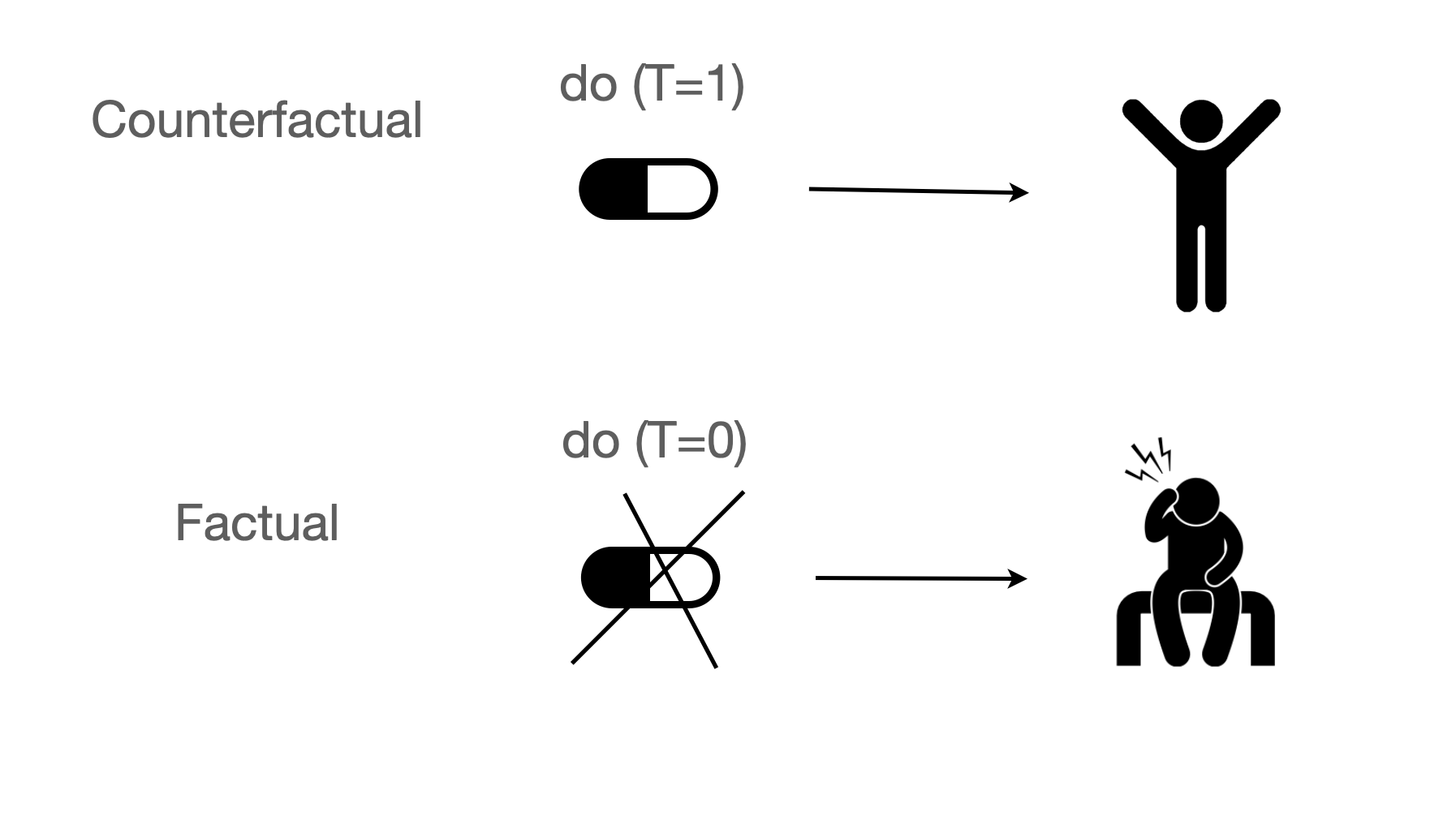
Source: Introduction to Causal Inference (ICI) by Brady Neal; The book of why by Judea Pearl

Statistical Inference